[IA Series 5/n] The Evolution from Logic to Probability to Deep Learning: A course correction to Transformers

Introduction

In the previous post, I shared my view on “Why Study Logic?”, we looked at the Knowledge Representation and highlighted the importance of Logic and Reasoning in storing and accessing Knowledge.

In this post I’m going to highlight a section from the book “Introduction to Artificial Intelligence” by Wolfgang Ertel. His approach with this book was to make AI more accessible than Russel and Norvig’s 1000+ page bible. It worked for me.

After that, I’ll touch on Reasoning with Uncertainty and then jump to Transformers (the architecture behind ChatGPT). It’s a jump because I’d thought it was the same, however in writing this, it’s clear that it isn’t!

I know see two types of knowledge base and one information store:

1. Symbolic Logic
2. Reasoning with Belief/Uncertainty
3. A Neural Network (which stores information rather than knowledge)

I really want to emphasis the difference between Neural Networks and Reasoning with Belief/Uncertainity. It’s the difference between the Probability Theory Rosenblatt used to create the first Artificial Neuron and Reasoning with Uncertainty. The stark truth is that Artificial Neurons aren’t reasoning, though it may seem like it to the end user, and this post will explain why.

First, let’s use logic to answer the question: “Do Penguins fly?”

Do Penguins Fly?

This is taken directly from the book, I like to think of the first sentence as a fundamental problem of using classical logic as for Knowledge Representation (rather than the more generic “fundamental problem of logic”)

With a simple example we will demonstrate a fundamental problem of logic and possible solution approaches. Given the statements

1. Tweety is a penguin
2. Penguins are birds
3. Birds can fly Formalised in PL1, the knowledge base KD results:

penguin(tweety)

penguin(x) => bird(x)

bird(x) => fly(x)

penguin(x) => ¬fly(x)

From there ¬fly(tweety) can be derived. But fly(tweety) is still true.

So there it is. Once a fact/assertion (i.e. a Sentence/well formed logical formula believed to be true) is in the Knowledge Base it cannot be negated. There are workarounds, check the book out for more information on those, what I will say though is that it involves excluding every bird that cannot fly when saying that birds can fly. A task that is probably intractable in you knew everything up front, and we do not know everything full stop!

This is where the term Monotonic becomes useful. Again I would word this differently, using the term “classical logic” rather than the generic term logic.

Here we notice an important characteristic of logic, namely monotony. Although we explicitly state that penguins cannot fly, the opposite can still be derived.

Plurality of logic

In the above example from Ertel’s book, I’ve highlighted how I’d have worded it differently. The main reason, and maybe it is because the book is translated from German to English, is that it is misleading if you do not know about the plurality of logic.

There are many forms, I do not fully know the differences, however I understand that John McCarthy tried to solve this problem by creating a Non-monotonic Logic, whilst it was successful as a Theoretical concept the computational implementation was intractable.

Claude has given me plenty of papers to look at, to get an understanding of the details, papers which I don’t have time to read diagonally yet. However, I like to look at the timeline of events to get a feel for how this all panned out. I’ll update this when I do have time.

Problems with using logics to store knowledge

• Frame Problem (McCarthy & Hayes, 1969): Difficulty in expressing what remains unchanged when actions occur
• Qualification Problem (McCarthy, late 1960s): Challenge of listing all preconditions for an action to succeed
• Brittleness Issues (1970s): Early expert systems failed when encountering situations outside their rule sets
• Monotonic Reasoning Limitations (1970s): Classical logic couldn’t retract conclusions when new contradictory information emerged
• Non-monotonic Reasoning (McCarthy, 1980): Proposed as a solution to allow conclusion retraction
• Default Logic (Reiter, 1980): Formalised reasoning with default assumptions
• Computational Intractability (late 1980s-early 1990s): Implementation attempts revealed non-monotonic logics were theoretically elegant but practically inefficient

Is there a solution to logic’s knowledge problem?

• Non-monotonic Reasoning Proposals (McCarthy, 1980): Introduced to address limitations of classical logic
• Default Logic (Reiter, 1980): Formalised reasoning with default assumptions
• Circumscription (McCarthy, 1980): Method for minimising abnormality in logical reasoning
• Truth Maintenance Systems (Doyle, 1979): Managing beliefs and their justifications
• Implementation Challenges (late 1980s-early 1990s): Non-monotonic logics proved computationally expensive
• Theoretical vs. Practical (early 1990s): Despite mathematical elegance, pure logic-based systems struggled with real-world complexity

Reasoning with Uncertainty

There’s quite an elegant solution to continuing using computers to reason, one that rings true for those that identify as Bayesian, and see probability as an expression of belief…

Belief as a measure of (un)certainty

Instead of saying that all birds can fly or not, the true or false, we can assign a strength of belief that all birds can fly. So, given a bird (any bird) I’d say theres over a 99% change that bird can fly.

P(fly|bird) = 0.99

Et voila, you have a Sentence that covers birds flying and it can be Reasoned with in a Bayesian Network.

Maximising Entropy: Bridging gaps in knowledge

There’s another approach, which Ertel covers in Chapter 7. Instead of using a Bayesian Network, the Principle of Maximum Entropy can be used to “fill in the gaps” on the probability distribution. It does this by treating the current knowledge (e.g. P(fly|bird) = 0.99) as a constraint and then maximising the entropy in the probability distribution. Like the opposite of Gradient Descent.

Jaynes introduced the Maximum Entropy Principles in 1957 and the approach had some bumps, however it has been used in a medical system from the late 1990s to at least 2010 (when the book was published). The lexmed.de site is no longer functional but there is some 3rd party information available here on the website of the Institute of Applied Sciences at the University of Applied Sciences Ravensburg-Weingarten.

I would like to go into this more, and create one, however I’m asking the wrong question. It isn’t Why Study Logic in a World of Probabilistic AI? It should be Why Study Logic in a World of Transformers?

The Transformer Revolution: A New Kind of Reasoning?

Part of the reason I have been short in covering Reasoning with Uncertainty is that the field is larger than I had realised. The books are great if you are interested in learning about it and there are a lot of really cool things that can be done - I’d like to get to creating a Hidden Markov Model that acts as a Sensor. That I will not be doing in a couple of days. And these two posts have been about Why Study Logic in a World of Probabilistic AI Transformers?

The other reason is that, when I started these posts, it wasn’t clear to me the difference between what a Transformer does and Probabilistic Reasoning. In my mind Transformers were producing a Probability Distribution of the most likely next token, therefore it was maybe Reasoning with Probability… The above section is shorter because it’s not doing that. I do not (yet) know what is it doing, people say pattern matching but that feels wrong still…

The question that I have been heading towards (though it wasn’t clear to me until now) is has the Transformer replaced Logic-based systems?

I mean this as a serious hype-free question, with my best Mathematical hat on. And breaking it down:

• Are Embeddings a logic? Can Vector Arrays be considered Symbols? Math is called a language… and this arithmetic works king - man + woman ≈ queen in Vector Space
• Can we consider the Attention mechanism of the Transformer architecture Reasoning? It cross references each token in a sentence and extracts meaning… Remember the definition of Reasoning? the action of thinking about something in a logical, sensible way well the attention mechanism is logical and sensible!
• Are these coming together to store knowledge as weights and biases in the Neural Network??

I’ve been pretty convinced but not certain. Maybe running with a belief based Probability of 0.75, that is P(LLMS_Reason|My_Observation) = 0.75

Vector Spaces as Symbolic Environments: Testing the Laws of Thought

I missed something from the definition of Logic in the previous post. Let’s look at what Wikipedia says about Logic

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term “a logic” refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Sure it touches on what was originally confusing for me - that Logic means different things, and there are many different types with different objectives.

Now I could argue that this is what a Transformer is doing with the tokens it receives.

Logic studies arguments, which consist of a set of premises that leads to a conclusion.

Reasoning is the activity of drawing inferences.

Definitely this one:

An argument is a set of premises together with a conclusion.

Premises are the prompts (System and User), the Conclusion is the Response. Voila.

OK, I’m convinced (not really but I wanted to write some code and get a picture), let’s look at the Vector Space as a logic

Formal logic (also known as symbolic logic) is widely used in mathematical logic. It uses a formal approach to study reasoning: it replaces concrete expressions with abstract symbols to examine the logical form of arguments independent of their concrete content.

If the embedding space is fixed, why is that now a Symbolic Logic? Numbers are symbols and we know we can perform arithmetic on them. king - man + woman ≈ queen

The word “logic” originates from the Greek word logos, which has a variety of translations, such as reason, discourse, or language.[4] Logic is traditionally defined as the study of the laws of thought or correct reasoning,[5] and is usually understood in terms of inferences or arguments.

So let’s look at the Laws of Thought

1. The law of identity: P -> P is TRUE.
2. The law of noncontradiction: P AND ¬P is FALSE.
3. The law of the excluded middle: P OR ¬P is TRUE.

The law of identity

I interpret the law of identity to mean that every time you convert “Penguins can fly” to a Vector you get the same result. The Embedding models need to be deterministic, for this post I’m taking it that they are (certainly practically though it probably needs to be proven)

The law of noncontradiction

This opens up to what is True or False in vector space - it’s continuous and I’m starting to understand why we need to study logic. How can we prove that “Penguins can fly” AND “Penguins cannot fly” is False?

Given the vector addition has some interesting properties, let’s add them together and see if they are zero. Because zero is good for False in programming. As I’m not sure, let’s look at them being opposite of each other as well.

• Perfect opposites would have a sum norm of 0
• Their cosine similarity would be -1.0

Oh they aren’t opposite via Cosine nor do they sum to zero…

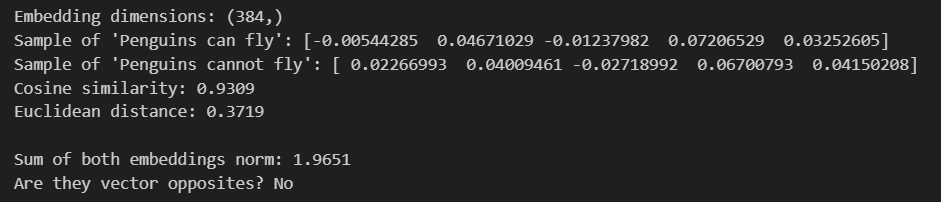
So this is it… We can say it obeyed the law of identity but there’s no way to say that it obeys the law of non-contradiction. Or is there?

4th Quarter stoppage time Hail Mary

Let’s look at there position in vector space - it’s 384 dimensions so we’ll look at it in 2 dimensions using Principle Component Analysis.

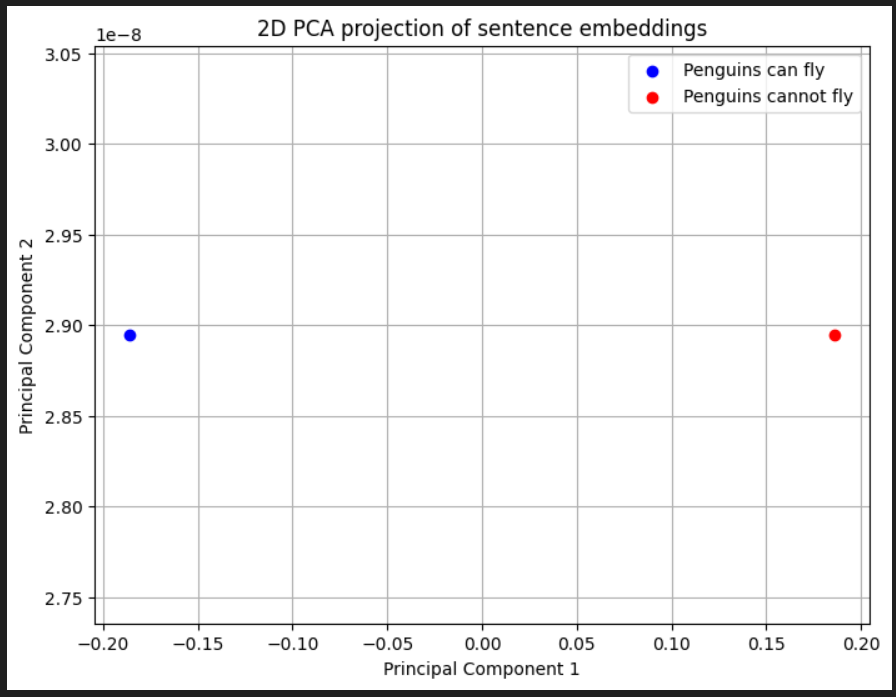
wow - they are opposite of each other…. well the 2 main components are.

Conflicting views here but, having learnt a bit of logic, a TRUE AND FALSE is FALSE…

Still that’s interesting. Can we say that there is an element of negation and therefore logic local to the region of “penguin” and “fly”?

The code for the above

I’ll make it available in my Intelligent Agent repo

Conclusion

In writing this an answer to the big question of Why Study Logic? has become clear for me.

It’d be great if what I’ve written helps others as well, sorry if it’s a bit rushed. I’ve been writing as I’m reviewing my notes, in an ideal world I’d have reviewed these as well so I expect some inconsistency.

And to share what I think the answer is to that question; Study Logic to know what a good system should be able to do. Maybe you won’t use it directly, but it’s the foundation of Knowledge and sensible reasoning so has clear value. Me, I’m glad to have dug in to understand a more common vocabulary and iron out some clearly wrong or incomplete beliefs that I had.

Going forward, I’d like to see if an Embedding Vector Space could be made that obeys the laws of logic.

Given what I’ve read about the using Probability Theory to reason, I think the vector space would need to be normalised, say between 0 and 1 so vectors could be treated in a similar to how Reasoning with Uncertainty treats probabilities. Maybe they are already normalised. The reduction of the “Penguins can fly” and “Penguins cannot fly” embeddings to 2 dimensions was very interesting.

For me, in those dimensions there was clear symmetry (if not opposites). That’s definitely something I’ll mull over. Another thing that may be interesting is to do is add and subject the vector for “not” to test embeddings, what is the consequence of that? logical operators for Vector Space?

Thanks for reading, Matt